线性回归完全指南:从理论推导到实例应用
目录
基本概念
在统计学中,线性回归(英语:Linear Regression)是利用称为线性回归方程的最小二乘函数对一个或多个解释变量和被解释变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个解释变量的情况称为一元回归,大于一个解释变量情况的叫做多元回归(multivariable linear regression)。[1]
注:在经济学中,自变量也被称为解释变量,因变量也称为被解释变量。同时存在多个自变量的情况下,还会将自变量分为核心解释变量和控制变量,但需要注意的一点是,这种区分是人为区分的,在估计参数时,统一将其当作自变量处理。在本文当中,会统一使用解释变量和被解释变量的称呼,需注意。
举个例子:想象你是一位房产中介,你发现房子面积越大,价格似乎越高。你想量化这种关系,这就是线性回归要解决的问题,分析解释变量对被解释变量的变化的可以解释程度。
线性回归的核心思想是:用一条直线(或超平面)来描述解释变量(X)和被解释变量(Y)之间的关系。比如上述例子中,这条直线的方程可以表示为:
其中:
- $Y$:被解释变量(如房价)
- $X$:解释变量(如面积)
- $\beta_0$:截距项(当 X=0 时 Y 的值)
- $\beta_1$:斜率(X 每增加 1 单位,Y 的变化量,也就是 X 对 Y 的变动的解释程度)
- $\varepsilon$:误差项(模型无法解释的部分)
如下图所示,其中红色的线为回归线$ Y = \beta_0 + \beta_1X + \varepsilon$,蓝色的点为真实值。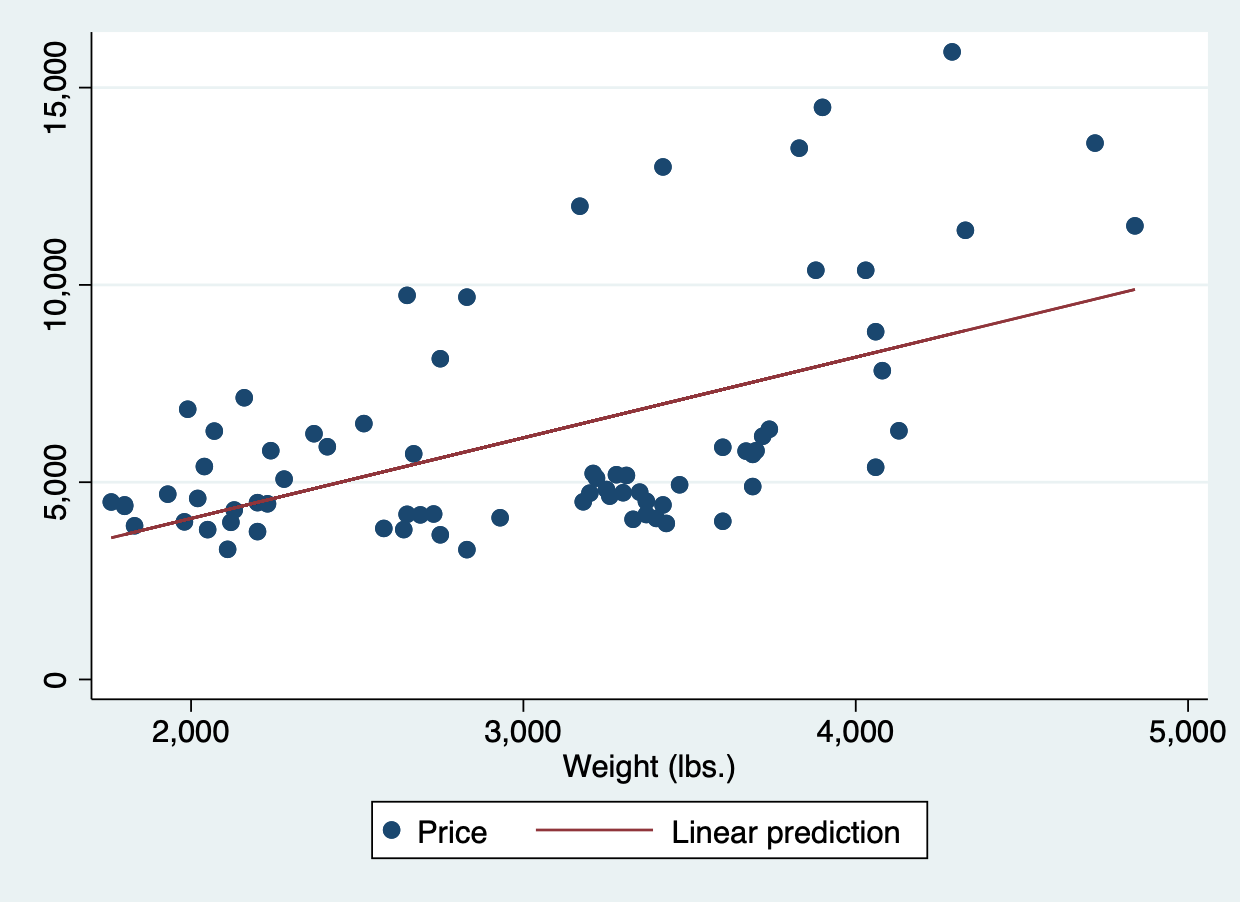
注:其实从这个地方也能看得出来,线性回归本身描述是真实值$Y$的趋势,也可以说是$Y$的均值的预测,并不是对每个真实值的准确预测,这并非线性回归的目的。即给定$X_i$的条件下,$Y_i$的均值是多少,即$E(Y_i | X_i)=Y$。线性回归这种特性是为了可解释性而存在的。例如各种深度学习模型,比如CNN、LSTM等,他们的预测能力可能非常强,但是可解释性并不那么高,这种模型还是个黑匣子,对每个变量的参数是不可控的。而线性回归模型不一样,只要模型形式确定了,数据确定了,那无论什么时候,模型的参数都是确定的,同时也是可以直接量化的。
若你认为价格不仅可以被面积影响,还有其他因素,那么可以通过添加其他解释变量来提高回归模型的预测效果,如当地的经济发展水平,地区人口密度等,那你的模型就可以表示为:
其中:
- $Y$:为被解释变量:房价
- $X_1$:解释变量 1:面积
- $X_2$:解释变量 2:本地经济发展水平
- $X_3$:解释变量 3:地区人口密度
- $\beta_0$:截距项(当 X=0 时 Y 的值)
- $\beta_i$:斜率($X_i$每增加 1 单位,Y 的变化量)
- $\varepsilon$:误差项(模型无法解释的部分)
其中$(1)$和$(2)$分别为一元线性回归和多元线性回归。
模型设定
更一般的,线性回归被表示为:
若令:
则线性回归就可以被简洁的表示为:
参数推导
不少人会对线性回归有所疑惑,模型数学表达式知道了,那么如何推导出参数呢?其实参数的推导是来自于数据本身的,也就是说,参数是根据数据所决定的,而不是模型所决定的。更通俗点就是由$Y、X$所决定的,于是下面让我们来推导一下参数的基本表达式,以一元线性回归为例,假设真实模型为:
估计模型为:
其中$\varepsilon$为误差项,$X$为解释变量,$Y$为被解释变量,$\hat{Y_i}$为模型预测的被解释变量值,在数学中,通常将$\hat{\phantom{a}}$来表示一个变量的估计值或预测值。
又:
拟合的目标就是想要让,预测值$\hat{Y_i}$与实际值$Y_i$尽可能小,
得到最小二乘目标函数:
对$\beta_0, \beta_1$分别求偏导数,并使其等于 0,得到:
对其进行求解,就可以得到下列参数方程。
一元线性回归参数方程:
其中 $\bar{X}$和$\bar{Y}$为样本均值。
多元回归的推导更加复杂,但逻辑和上述回归一样,这里不再推导。
假设条件
1.线性关系假定
线性回归模型假定,$Y$与$X$之间的关系为参数线性关系,即$(3)$式,若形式为:
该模型仍然是线性关系,但若形式为:
则该模型不再满足线性关系,因为参数$\beta_2$并不是一次幂,于是参数就无法使用 OLS 估计了。简单来说,该假定强调了模型的参数必须是一次幂,而不限制变量的幂。例如:
仍然是满足线性关系假定的,这种模型也被称为双对数模型,在实践中也经常被使用,因为该模型表达了解释变量$X$对被解释变量$Y$的边际效用。
例如经济学中经典的生产函数柯布-道格拉斯生产函数,其数学表达式为:
对两边取对数,可以得到:
通过对数变换,就可以将非线性模型转换为线性模型。
2.误差项零均值假定
该假定义为:$E(\varepsilon) = 0$,从最小二乘法的推导过程中可以看到,我们的目标就是使得残差的平方和最小。在$(8)$式中,$\beta0 = 2\sum{i=1}^n (Yi - \beta_0 - \beta_1X)=0$,其中其实就是让残差之和为零,又残差项均值为$\bar\varepsilon=\frac{\sum{i}^n \varepsilon}{n}$,所以$\bar\varepsilon=0$。上面谈到$E(Y_i | X_i)=Y$,因此,可以得到$E(\varepsilon | X_i)=0$,即残差项的期望为零,又$E(\varepsilon)=E(E(\varepsilon | X_i))=E(0)=0$,因此,残差项的期望为零。在模型的构建中,也常用这个来检验模型的构建是否正确。
stata代码实操:1
2
3
4
5
6
7
8sysuse auto, clear // 导入 stata 自带数据
reg price weight // 线性回归:price = β0 + β1*weight + ε
predict y_hat, xb // 生成预测值 (ŷ = Xβ̂)
gen resid = price - y_hat // 计算残差 (ε̂ = ŷ - y)
sum resid, detail // 残差描述性统计
di %9.2f r(sum) // 显示残差和(保留2位小数)
0.00 // 这个地方就是残差和
可以从上面的回归结果发现,残差和正好为 0,这里保留 2 位小数是因为stata 在计算过程中,可能会因为精度的不同,结构会有些许误差。
3.多重共线性假设
该假定假设当模型存在多个解释变量时即当模型是多元线性回归的时候,这些解释变量之间不存在完全的线性关系。这是因为当模型的多个变量存在完全的线性关系时,模型参数将无法估计。假定模型为:
则可以发现,$X_2$和$X_1$之间存在完全的线性关系,则$(15)$式可以变为:
其中$\beta = \beta_1 + \alpha\beta_2$, $\varphi = (\beta_2 + 1)\varepsilon$。
可以发现,$X_2$的存在是没有意义的,因为$X_2$对$Y$的贡献已经由$X_1$的贡献所代替。在 stata 中,若存在完全的多重共线性,模型会将其忽略掉,显示下面的结果:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20sysuse auto, clear # 载入数据
rename weight x1 # 重命名变量为x1
gen x2 = 1 + 2 * x1 # 生成变量x2,x2 = 1 + 2 * x1
reg price x2 x1
note: x1 omitted because of collinearity.
Source | SS df MS Number of obs = 74
-------------+---------------------------------- F(1, 72) = 29.42
Model | 184233937 1 184233937 Prob > F = 0.0000
Residual | 450831459 72 6261548.04 R-squared = 0.2901
-------------+---------------------------------- Adj R-squared = 0.2802
Total | 635065396 73 8699525.97 Root MSE = 2502.3
------------------------------------------------------------------------------
price | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
x2 | 1.022031 .1884171 5.42 0.000 .6464287 1.397634
x1 | 0 (omitted)
_cons | -7.729385 1174.612 -0.01 0.995 -2349.276 2333.817
------------------------------------------------------------------------------
可以看到,$X_2 =1 + 2*X_1$,这个是$X_1$变量是存在完全的多重共线性关系的,于是 Stata 会自动忽略掉该变量。而在其他的程序中,可能会出现错误,比如在 python 中:
1 | # 导入包 |
可以发现在上面,也报出了多重共线性的错误。
4.同方差假设
该假设说明了误差项的方差是是一个常数,即$Var(\varepsilon|X) = \sigma^2$,它不应该随误差项的改变而改变,这是为了确保普通最小二乘法(OLS)的标准误估计有效,从而保证假设检验(t 检验、F 检验)和置信区间的准确性。
5.误差项无自相关
该假设说明了误差项之间不存在自相关关系,即$Cov(\varepsilon_i | \varepsilon_j) = 0, (i \neq j)$。简单来说,就是误差项应该是随机的,而不是具有相关性的。
6.外生性假定
该假设是说,解释变量与误差项不存在相关关系,即$Cov(X_i,\varepsilon_i)=0$,进而$E(\varepsilon_i | X)=0$,排除遗漏变量偏差和双向因果关系,确保 OLS 估计量的一致性和无偏性。
7.误差项正态性
该假设是说,误差项是服从正态分布的,即$\varepsilon_i \sim N(0, \sigma^2)$。其中$\sigma^2$为误差项的方差。该假设由同方差假设和均值假设组成。
为了文章的简洁性,各种假设的检验方法,我将在后面的文章中详细介绍。
最小二乘法统计性质
之所以线性回归会使用最小二乘法$(OLS)$估计方法,是因为其具备良好的统计性质,主要包括线性性、无偏性、一致性,即在经典假设下,OLS是 最优线性无偏估计(BLUE),也称高斯-马尔可夫定理。
- 线性性
线性性是指利用 $OLS$ 估计出来的参数是观测者$Y$的线性组合。从式$(9)$就可以看出来。参数$\beta_i$都是$Y$的线性组合。 - 无偏性
无偏性是指,参数的估计值$\hat\beta_i$的期望与参数的真实值$\beta_i$相同,即$E(\hat\beta_i) = \beta_i$ - 一致性
即 OLS 估计参数在所有的无偏线性估计里面,具备最小方差性。
模型评价
符号规定:
- $n$: 样本数
- $k$: 参数个数(不包括截距项)
- $y_i$: 被解释变量真实值
- $\hat y_i$: 被解释变量估计值
- $\bar y$: 被解释变量的均值
残差平方和$RSS$
定义:含义:残差平方和,他表示了模型未能解释的部分,即估计的(\hat yi) 与真实值(y_i) 之间的距离。
自由度:$df{RSS} = n-k-1$回归平方和$ESS$
定义:含义:回归平方和,表示模型解释的部分。
自由度:$df_{ESS} = k$(含截距项模型)总平方和$TSS$
定义:含义:总平方和,表示数据集的方差。
自由度:$df{TSS} = df{ESS} + df_{RSS} = n-1$
拟合优度$R^2$
定义:
其中,$R^2$为模型拟合程度,也被称作可决系数、拟合优度等。它表示回归模型对因变量波动的解释比例,即解释变量对因变量总变异的解释程度。。从这个角度也能看出,$R^2$的取值范围为$[0,1]$,越接近 1,说明模型解释程度越好,否则,模型解释程度越差。
注:$R^2$越大不一定越好。因为增加新的解释变量通常会导致$R^2$增加,即使这些变量与因变量关系不大;
调整后的拟合优度$\bar R^2$
定义:
$\bar R^2$是调整后的可决系数,这是因为拟合优度$R^2$计算存在一些缺陷,$R^2$会受到模型解释变量的个数的影响,也就是说,只要通过增加解释变量的个数,就可以在一定程度上使得$R^2$增加。但是假设3提到,模型的解释变量之间不能严重的存在多重共线性,因此,$\bar R^2$就增加了一个对$R^2$的修正,使得$\bar R^2$在增加解释变量个数时,会对$R^2$施加一定的惩罚系数。因此使用$\bar R^2$有助于一定程度上抑制无效变量的引入,增强模型的稳健性和可解释性。当新加入变量没有带来模型提升时,$\bar R^2$ 可能下降,防止过拟合。
注:选择使用哪个系数进行判断,需要根据实际情况选择。
假设检验
这里的假设检验并不是对各种假设条件的检验,而是对估计参数的统计检验,也就是通过统计学的方法来判断我们估计的参数是否有效,主要包括了 $t$ 检验和 $F$ 检验。
t检验
设原假设为:
备择假设(双尾检验)为:
注:若理论支持方向性,可改用单尾检验(如$H_1: \beta_i > 0$或$H_1: \beta_i < 0$)
即原假设假设解释变量对被解释变量不具备影响能力。备择假设则认为解释变量对被解释变量有影响。
其实可以发现,原假设和备择假设是对立的,在 t 检验中,我们假设原假设为真,然后通过构造t 统计量来判断,如果 t 统计量大于 t 值,则原假设被拒绝,否则原假设被接受。t 统计量计算公式为:
其中,$n-k-1$是自由度,$n、k$分别为样本量和解释变量个数,$\hat{\beta_i}$是系数的估计值,$\beta_i$为原假设的理论值,$SE(\hat{\beta_i})$是系数的估计标准差。在这里,原假设是$\beta_i = 0$,于是上式就可以变为:
得到 t 统计量后,我们首先要查表确定在这个自由度下的$t{\alpha/2}{(n-k-1)}$的临界值,例如,95%的显著性水平的双尾检验的$\alpha$ = 0.0),$t{\alpha/2}$(的临界值为2.262。
若我们计算得到的$|t| > t_{\alpha/2}$,则认为拒绝原假设,选择备择假设。否则,不能拒绝原假设。
或者使用 $p$值,查找计算出的 $t$ 统计量所对应的$p$值,若$p< \alpha$,则拒绝原假设,否则不能拒绝原假设。
在 stata 中可以通过以下命令实现:1
2
3
4
5
6. display invttail(20, 0.025) #其中20为自由度,0.025为α, 得到的是临界值
2.0859634
. display 2 * ttail(20, abs(4)) #其中 20 为自由度,4为 t 统计量,(若是双尾检验则需要*2,若是单尾则不需要),得到p值
.00070352
这一部分可以看代码实现部分,会没那么抽象。
F检验
F 检验主要用于检验多个解释变量之间是否同时满足某个条件,例如模型设为:
则 F 检验的原假设为:
备择假设为:
F 检验的统计量计算公式为:
其中:
- $RSS$为残差平方和;
- $ESS$为回归平方和;
- $k$为解释变量个数,即解释变量个数;
- $n$为样本个数,即样本个数。
F 检验实际上是在检验整个模型的有效性,若解释变量的系数均为 0,那么这个模型也就无效了,若起码有一个系数不为 0,那么这个模型仍然是有效的。这是一个很关键的点,
stata代码实现
我们使用 stata 自带的 auto 数据进行一次一元的线性回归分析,以 price为被解释变量,weight 为解释变量,设模型为如下形式:
其中$Y$为 price,$X$为 weight,$\varepsilon$为误差项。
首先打开 stata ,输入以下代码:1
2
3
4
5. sysuse auto, clear // 导入 stata 自带数据
(1978 automobile data)
.
end of do-file
这一步操作主要是导入数据 stata 自带的 auto 数据集,
接下来,输入以下代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22. rename price Y // 我们将price重命名为 Y(这一步非必需,只是为了符号统一)
. rename weight X // 我们将weight重命名为 X(这一步非必需,只是为了符号统一)
. reg Y X // 这一步是拟合模型,Y = β0 + β1*X + ε
Source | SS df MS Number of obs = 74
-------------+---------------------------------- F(1, 72) = 29.42
Model | 184233937 1 184233937 Prob > F = 0.0000
Residual | 450831459 72 6261548.04 R-squared = 0.2901
-------------+---------------------------------- Adj R-squared = 0.2802
Total | 635065396 73 8699525.97 Root MSE = 2502.3
------------------------------------------------------------------------------
Y | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
X | 2.044063 .3768341 5.42 0.000 1.292857 2.795268
_cons | -6.707353 1174.43 -0.01 0.995 -2347.89 2334.475
------------------------------------------------------------------------------
.
end of do-file
结果如上所示,现在我们来解析一下这个结果,首先看左上方的结果,如下所示,其中$Source$ 表示来源,$SS$ 为平方和,$df$ 表示自由度,$MS $表示均方差。第二行第三行分别表示模型和残差$SS$、$df$、$MS$,以及总$SS$、$df$、$MS$。1
2
3
4
5
6 Source | SS df MS
-------------+----------------------------------
Model | 184233937 1 184233937
Residual | 450831459 72 6261548.04
-------------+----------------------------------
Total | 635065396 73 8699525.97
然后再看右上方的结果,如下所示,其中$F(1, 72)=29.42$表示自由度为$(1, 72)$的$F$检验统计值为$29.42$,$P>F$ 表示$F$检验的$p$值,R-squared表示$R^2$值,即拟合优度(决定系数),Adj R-squared表示调整后的$R^2$值,Root MSE 表示根均方误差(回归标准误)。1
2
3
4
5
6Number of obs = 74
F(1, 72) = 29.42
Prob > F = 0.0000
R-squared = 0.2901
Adj R-squared = 0.2802
Root MSE = 2502.3
最后再来看下方的参数估计表,如下方所示,其中第一行为标头,分别表示被解释变量$Y$,Coefficient为解释变量的系数$\beta$的估计值,Std. err为$\beta$的估计值的标准误差,$t$为$\beta$的估计值的t统计量,$P>|t|$为$t$统计量的$p$值,[0.025, 0.975]为95%的置信区间其中,$X$行表示X的所有值,_cons为常数项。1
2
3
4
5
6------------------------------------------------------------------------------
Y | Coefficient Std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
X | 2.044063 .3768341 5.42 0.000 1.292857 2.795268
_cons | -6.707353 1174.43 -0.01 0.995 -2347.89 2334.475
------------------------------------------------------------------------------
于是通过上面的分析,我们可以写出如下的估计线性方程:
python代码实现
我们通过使用 sklearn 的鸾尾花数据集进行分析,得到下面的结果,解读方法和stata 的差不多,只是在这儿,常数是Intercept,coef 是系数,std err 是标准误差,Prob (F-statistic)是 F 检验的p值。更多的介绍将在后面分析。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43# 导入包
import numpy as np
from statsmodels.formula.api import ols
import pandas as pd
# 导入 sklearn 数据
from sklearn.datasets import load_iris
X, y = load_iris(return_X_y=True)
# 合并数据
data = pd.concat([pd.DataFrame(X), pd.DataFrame(y)], axis=1)
data.columns = ["x1", "x2", "x3", "x4", "y"]
# 构造多重共线性数据
# 模型拟合
model = ols('y ~ x1 + x2 + x3 + x4 ', data).fit()
print(model.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.930
Model: OLS Adj. R-squared: 0.928
Method: Least Squares F-statistic: 484.5
Date: Sat, 26 Jul 2025 Prob (F-statistic): 8.46e-83
Time: 14:39:31 Log-Likelihood: 17.437
No. Observations: 150 AIC: -24.87
Df Residuals: 145 BIC: -9.821
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.1865 0.205 0.910 0.364 -0.218 0.591
x1 -0.1119 0.058 -1.941 0.054 -0.226 0.002
x2 -0.0401 0.060 -0.671 0.503 -0.158 0.078
x3 0.2286 0.057 4.022 0.000 0.116 0.341
x4 0.6093 0.094 6.450 0.000 0.423 0.796
==============================================================================
Omnibus: 0.374 Durbin-Watson: 1.077
Prob(Omnibus): 0.829 Jarque-Bera (JB): 0.141
Skew: -0.051 Prob(JB): 0.932
Kurtosis: 3.110 Cond. No. 91.9
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
参考文献:
[1]. 维基百科编者. 線性回歸[G/OL]. 维基百科, 2025(20250705)[2025-07-05].
[2]. Wooldridge, J. M. (2010). Econometric Analysis of Cross Section and Panel Data.
[3]. Greene, W. H. (2012). Econometric Analysis.